馬可夫模型 (Markov Model) 會用來表達狀態以及轉移機率及它們的隨機過程使用的模型，或許在前面文章有兩個例子: 有限狀態機、有限狀態過程，馬可夫模型也是一種有有限狀態機，只是要把它箭頭指向的地方都當作是隨機指向；而且，馬可夫模型也是圖 (Graph)。

本文章不會細究隱式馬可夫模型 (HMM) 以及相關演算法 (向前向後、Viterbi…etc)。

讀馬可夫模型

本篇文章介紹馬可夫模型會以機率觀測的形式來介紹，也就是說，你會看到一個簡單的建模過程，也可以看到馬可夫模型的一些基礎元素。

比方說，現在下面要邊介紹元素邊用剪刀石頭布的例子來介紹【整體觀測機率模型】，就是對時間序列的每一局而言的狀態轉移機率。

要注意，這跟帶有時間序列的馬可夫模型不一樣，探討的主題就不同了，扯到時間序列就會偏離本文章主軸，畢竟【每一次遊玩】的第一局和第二局可能呈現與【整體】不一樣的狀況。

於是可能會取決於每一局玩剪刀石頭布的優勢情形。

狀態

狀態是你要觀測的元素，狀況就只有剪刀、石頭、布:

狀態轉移機率

假設你觀察你的對手數百次出拳情形，然後把它紀錄下來，會得到像這樣的一個小結論:

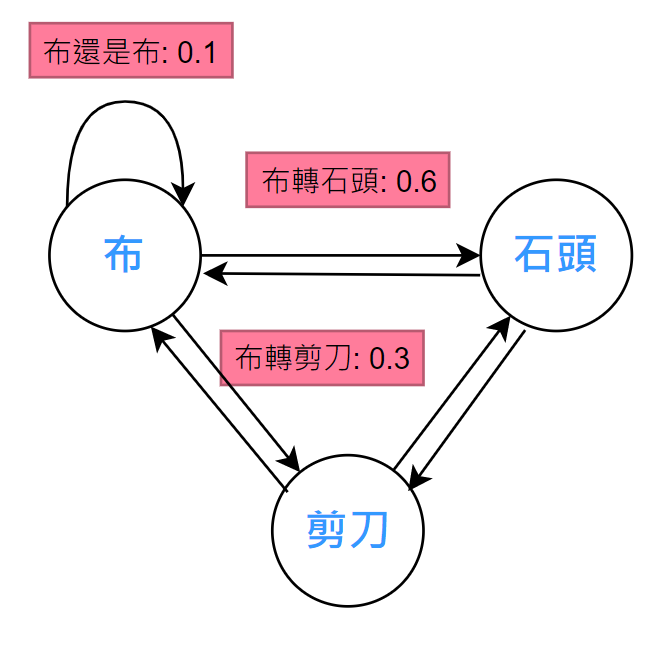
現在是針對【布】這個狀態，要預測下一個出拳情形，就可以直接參考，此預測他接下來會出【石頭】是最有可能的機率。

為什麼要特地指出布的所有機率，這是因為觀測機率建模必須包含布的所有可能性，稱為機率分佈，而機率分佈的總和必須是 1，這是為什麼上圖會做成 0.6, 0.3, 0.1 的機率的原因。

統計這個機率很簡單，你就是做簡單的統計平均數就可以實驗了，觀測每一次他出布之後，下一個出什麼，把出剪刀的總次數當作母數 (分母)，然後分別列出:

(布幾次) / (出布次數), (剪刀幾次) / (出布次數), (石頭幾次) / (出布次數)，以此類推，就可以得到整個模型的機率。

於是你知道箭頭、回到自己的箭頭是什麼意思，你就可以建出來像下圖一樣的機率模型:

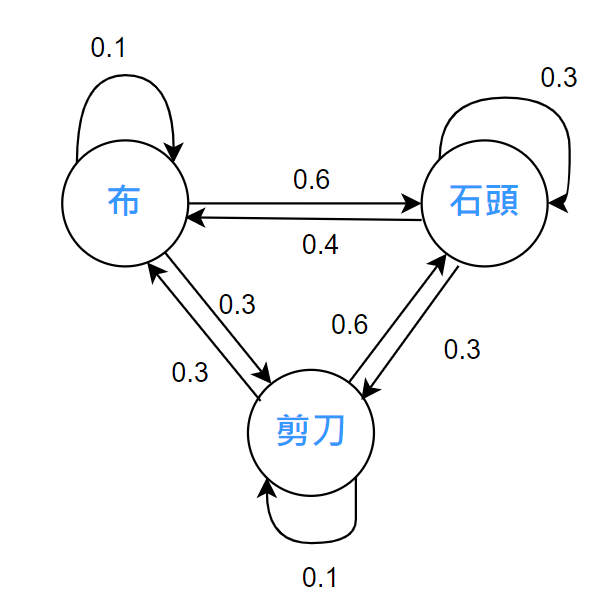
每個語言都可以實作馬可夫模型的機率轉移矩陣跟發生這些機率，在不使用第三方依賴套件的情況下，可能會寫出一個二維陣列:

transitionMatrixName = [
    ["A->A", "B->B", "C->C"],
    ["A->B", "B->C", "C->A"],
    ["A->C", "B->A", "C->B"]
]

transitionMatrixProbability = [
    [0.2, 0.6, 0.2],
    [0.1, 0.6, 0.3],
    [0.2, 0.7, 0.1]
]

transitionMatrixName 對應要描述的就是發生 X -> X 的事件對應的 transitionMatrixProbability 機率。

References:
[1] https://zh.wikipedia.org/wiki/%E9%A9%AC%E5%B0%94%E5%8F%AF%E5%A4%AB%E9%93%BE